Answer
-
The first matrix multiplication does not use tensor cores and the three remaining ones use tensor cores. This can be observed in the trace collected using Nsight Systems (nsys cli requires wrapping the code with
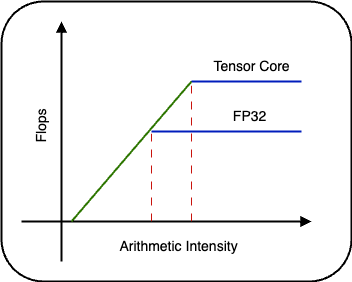
torch.cuda.cudart().cudaProfilerStart()andtorch.cuda.cudart().cudaProfilerStop()) or using the command line utility dcgmi.- Let $w$ denote the word size in bytes (4 for FP32, and 2 for FP16 and BF16). The arithmetic intensity of matrix multiplication is $\frac{2n^3}{3 w n^2} = \frac{2n}{3w}$ as there are approximately $2n^3$ operations required to multiply two square matrices of size $n$ and the number of reads and writes is $3n^2$.
- The machine balance is computed as the ratio of flops to memory bandwidth at the cusp in the roofline. The table below shows the machine balance for different numeric formats and $n=512$.
Numeric format Word size Machine balance Arithmetic intensity (2n/3w) FP32 4 19.5/1.55 ~ 12 ~ 85 TF32 4 156/1.55 ~ 100 ~ 85 FP16 2 312/1.55 ~ 201 ~ 170 BF16 2 312/1.55 ~ 201 ~ 170 Comparing the arithmetic intensity with the machine balance, we see that the first matrix multiplication is compute bound and the remaining three are memory bandwidth bound.
-
bf16 has 8 bits for the exponent and 7 bits for precision. On the other hand, fp16 has 5 bits for the exponent and 10 bits for precision. Since the matrix $A$ is initialized with random values between 0 and 1 and the exponent is $0$ the fractional part of bf16 compared to fp16 is 3 bits less. As $2^3 = 8$, the accuracy loss is 8 times when using bf16.
Discussion
How is a CUDA core different from a tensor core?
A CUDA core is a hardware unit that does scalar floating point operations. A Tensor core is a hardware unit that multiplies fixed size matrices - because it’s specialized to matrices, it can use a technique called “systolicization” to get very high throughput.
Is there a difference between fp16 and bf16?
There’s no difference in FLOPS/sec between fp16 and bf16, both for Tensor cores and CUDA cores. (This is subject to the assumption that there’s no type conversions.) Numerically, fp16 is superior to bf16 when values are small (as we saw in Puzzler 2). When dealing with larger values, bf16 becomes numerically superior (since there’s less likelihood of over/underflow.)
When are tensor cores utilized?
Tensor cores are automatically utilized when doing matrix multiplication but the performance (flops) achieved by the tensor cores is highly dependent on the matrix sizes and precision format.
| Numeric Format | cuBLAS ≥ 11.0 and cuDNN ≥ 7.6.3 |
|---|---|
| INT8 | Always but most efficient with multiples of 16; on A100, multiples of 128. |
| FP16 | Always but most efficient with multiples of 8; on A100, multiples of 64. |
| TF32 | Always but most efficient with multiples of 4; on A100, multiples of 32. |
| FP64 | Always but most efficient with multiples of 2; on A100, multiples of 16. |
See here for more details pertaining to different matrix instruction formats.
As an example, consider a transformer based language model built by stacking several encoder/decoder layers. We summarize below the limitations of using tensor cores for each layer used in the transformer architecture during the training phase.
| Operation categories | Uses tensor cores | Usually bound by |
|---|---|---|
| Matmul | Yes | Compute |
| Elementwise (Activation) | No | Memory bandwidth |
| Reduction(Pooling) | No | Memory bandwidth |
How can good utilization of tensor cores be ensured?
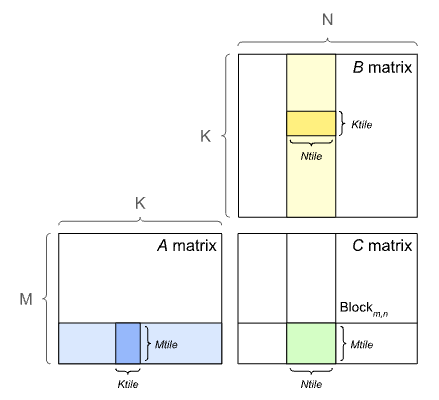
In order to extract better performance from the GPU, matrix multiplication of large matrices is broken down into smaller tiles as shown below:
Some common tile sizes are:
- 256x128 and 128x256 (most efficient)
- 128x128
- 256x64 and 64x256
- 128x64 and 64x128
- 64x64 (least efficient)
When the output matrix dimensions ($M, N$) are not evenly divisible by the tile size or the number of thread blocks are not evenly divisible by the number of Streaming Multiprocessors (SM) then there are wasted cycles which lead to inefficiency.
Tile Quantization
Tile quantization means that the work is quantized to the size of the tile. It happens when the matrix dimensions are not evenly divisible by the thread block size.
Wave Quantization
Wave quantization means that the work is quantized to the size of the GPU. It happens when the number of thread blocks is not evenly divisible by the number of SMs.
What should you remember in years to come?
Tensor cores and quantization/mixed precision can give you huge performance gains on a GPU. Choosing the correct matrix dimensions is critical to achieving maximum throughput.
Explore more
-
To see tensor core activity, collect a trace for a PyTorch program using Nsight Systems. Here’s a command to get you started:
nsys profile --stats true -o report_name --gpu-metrics-device=all python3 file_name.py -
Measure tensor core usage using DCGMI:
dcgmi dmon -e 1004